                 |
在完成了前两步之后,我们只剩下顶面的4个棱和4个角需要还原。这时魔方一共有多少种变化呢?简单说吧,就是
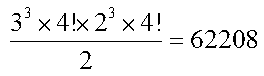
大家应该理解吧,最后分母上的2表示,角加棱的排列应该是个偶排列,或者是必须经过偶数个两两交换还原。呵呵,我说话越来越不明白了。
这里呢,Fridrich
System显然把这62208种状态分成了2步,也就是Orientation和Permutation,也就是我们的第三步,第四步。第三步将顶面的绿色的朝向调好了,这说明啥子呢?说明角块的朝向对好了,棱块的朝向对好了,也就是上面公式里33*23的部分,所以第三步有216种状态;第四步是4!*4!/2=288种状态。
第三步,我们只关心角和棱的朝向,顺序我们一点也不关心。
第四步。朝向对好了,我们只关心顺序。
所以下面的概率变得比较明显了。对于每一种形态,他的变异有多少种主要源自围绕中心的4个旋转的位置和左右或者上下的镜像产生的不同朝向配置。
我们应该发现具有越高对称性的形态,他的概率越低,为啥?因为在各种变换(旋转,镜像)下,都只得到他自己。
| 形态 |
算出概率的原因 |
出现概率 |

| 108说明有2个状态,就是旋转后会呈现的2个不同状态。他具有x,y两轴的镜像对称。 |
1/108 |

| 4个状态,就是旋转的4个状态,它具有上下对称。 | 1/54 |

| 8个状态,旋转4*左右对称2。不具任何对称 |
1/27 |

| 4个状态,旋转可得。对角线对称。 | 1/54 |

| 左右对称 | 1/54 |

| 左右对称 | 1/54 |

| 全对称,只有一个状态。 | 1/216 |

| 两轴对称。 | 1/108 |
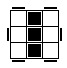
| 两轴对称 | 1/108 |

| 左右对称 | 1/54 |

| 左右对称 | 1/54 |

| 全不对称 | 1/27 |

| 全不对称 | 1/27 |

| 全不对称 | 1/27 |

| 全不对称 | 1/27 |

| 全不对称 | 1/27 |

| 全不对称 | 1/27 |

| 全不对称 | 1/27 |

| 全不对称 | 1/27 |

| 全不对称 | 1/27 |

| 全不对称 | 1/27 |

| 全不对称 | 1/27 |

| 全不对称 | 1/27 |

| 对角线对称 | 1/54 |

| 全不对称 | 1/27 |

| 对角线对称 | 1/54 |

| 上下对称 | 1/54 |

| 上下对称 | 1/54 |

| 全不对称 | 1/27 |

| 左右对称 | 1/54 |

| 左右对称 | 1/54 |

| 全不对称 | 1/27 |

| 两轴对称 | 1/108 |

| 上下对称 | 1/54 |

| 上下对称 | 1/54 |

| 上下对称 | 1/54 |

| 对角线对称 | 1/54 |

| 全不对称 |
1/27 |

| 对角线对称 |
1/54 |

| 两轴对称 | 1/108 |
大家发现了吧,凡是有一轴对称的就是1/54,对应4个状态,有两轴对称的就是1/108,对应两个状态,全对称的就是1/216,对应一个状态,全不对称的是1/27,对应8个状态。共计有
17*1/27 + 17*1/54 + 5*1/108 + 1/216=215/216
再加上1/216对好的情况,正好归一化。
对于第4步
我们看还有4!*4!/2=288种变化。这些变化就是4个角和4个棱的排列。
在下表中你会看到具有最高对称性的概率是1/72,这是因为,我们总可以用旋转的4个位置产生4种不同的变化。具有2轴对称性的就是1/36,他们一定交换两对东西,这两对东西的组合只有2种选择。具有一轴对称性的就是1/18,他们交换两对东西,这两对东西的组合有4种。不具有对称性交换两对东西是1/9,他们有镜像,加上每种镜像都有4种旋转,所以是2镜像*4选择*4旋转=32种变化。还有轮换3个东西,是1/9,因为选择有C(3,4)种,而又有顺逆时针两种镜像,加上4旋转。注意这种情况逆算法是可以等效于镜像算法的。
最后一个N情况比较特殊,因为他是唯一一个在旋转180的时候会产生出自身的pattern的情况,另外他的可选组合有4种,有2种在旋转中会呈现,所以最后剩下的概率就是1/72*4/2=1/36,这种情况很特殊。
最多的就是轮换2组的3个东西,也就是G情况。首先他不对称,有镜像,而且一个关键问题是他的逆算法和镜像算法不等效。这样就又多出一个2倍。这样就是逆算法2*镜像2*4选择*4旋转=64种变化。所以是2/9。呵呵。
你会有一个自然的疑问,为啥2组的3轮换,只有4种选择,明明是4*4=16种嘛,两组可以任意选择嘛,C(3,4)^2嘛!还有不管是镜像还是逆算法,2种旋转的方向总是相反的为啥不能顺着转呢。呵呵,如果你有这个疑问,说明你很棒!
首先,对于为啥选择不是4*4=16种。

比如这样,呵呵,你吧他转180度,你就会发现他会变成G2的情况,就是G算法的镜像算法。
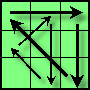
再比如这样,这时你会发现两个旋转是同方向的了。顺时针转90度你会发现他变成了R算法镜像算法。
这个主题应该还可以延伸,不过我现在有点困了。
| 名字 |
变换方式 |
算法 |
出现概率 |
| U |
|
(9,12,7,4) R² U Fs R² Bs U R²
|
|
1/9 |
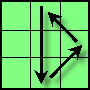 |
水平中线(上下)镜像:R² U' Fs R² Bs U' R² |
|
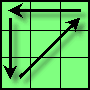
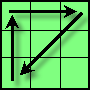
| A |
|
(9,12,9,3) L F' L B² L' F L B² L²
|
|
1/9 |
 |
对角线镜像:B' R B' L² B R' B' L² B² |
|
| Z |
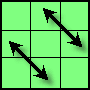 |
(12,18,7,6) Ls Ds2 Ls D Ls2 U' Bs2 | |
1/36 |
| (12,13,11,3)
R' F R Ba' R Fs R F' R' B2 (U3) |
|
| H |
 |
(10,12,10,5) Ra U² Ra'Fa'U² Fa |
|
1/72 |
|
(9,17,7,5) R2 Bs2 L² D' R² Bs2 L²(U) |
|
| E |  |
(14,14,14,4)
R B L B' R' Fa R F' L' F R' Fa' | | 1/36 |
| (15,16,15,4)
F R' F' L F R F' L² B' R B L B' R' B |
|
| T |
 |
(10,16,10,5)
(U3)L² D F² D' L² B² D' R² D B² |
|
1/18 |
| (14,15,14,3)
R B U' B' U B U B² R' B U B U' B' |
|
| V |
 |
(15,17,15,3)
L' U R U' L U L' U R' U' L U² R U² R' |
|
1/18 |
| (14,15,14,5)
F' U F' U' R' D R' D' R² F' R' F R F |
|
| (14,19,14,4)
(U2)B U B² R B² U' B' R² F'U F R² U² R' |
|
| F |
 |
(14,17,14,5)
L² F' L D² R' B R D²L B L F L' B' |
|
1/18 |
|
(13,18,12,6)
(U3)R' L F² L D' R F² L' U R² L' B² R² |
|
| (13,17,12,6)
(U2)B L' F U² B'R B' F² D² F² R' B F' |
|
| (16,16,16,4)
(U1)F R U' B U F' B' U B U' F R' F' R B' R' |
|
| R |
 |
(13,14,13,4)
(U')B' U² B U' R' F R B' R' F' R U' B |
|
1/9 |
|
(13,17,13,5)
(U2)R' F² L² D' L D L F² R U² L U' L' |
|
|
(14,15,14,3)
F L U L' F L U' F U F U'F'L'F² |
|
 |
左右镜像:
(U)B U2 B' U L F' L' B L F L' U B' |
|
| 左右镜像:
(U2)L F2 R2 D R' D' R' F2 L' U2 R' U R |
|
| 左右镜像:
F' R' U'R F 'R' U F' U' F' U F R F2 |
|
| J |
 |
(10,13,10,5) B2 L U L'B² R D' R D R² |
|
1/9 |
|
(10,12,10,3) (U') Fa U² B' U' B U² F' U B' |
|
 |
左右镜像:B2 R' U' R B2 L' D L' D' L2 |
|
| 左右镜像:(U)Fa' U2 B U B' U2 F U' B |
|
| Y |
 |
(13,15,13,5)
R B U' B' R D B' L' B' L B² D' R² |
|
1/18 |
|
(14,15,14,4)
(U2)L²U L' F L U' L' U' F' U' L' B' U B |
|
| (13,18,13,4)
(U3)B L B' R² B L' B' U² R² U' R² U' R² |
|
| G |
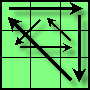 |
(12,14,12,5)
(U2)L U' R U² L' U R' Fa' U² Fa
|
|
2/9 |
|
(12,14,12,5)
F U F' L² D' B U' B' U B' D L² |
|
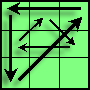 |
左右镜像:(U2)R' U L' U2 R U' L Fa U2 Fa' |
|
|
左右镜像:F' U' F R2 D B' U B U' B D' R2 |
|
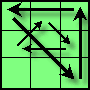 |
逆算法(倒序并每步取反):
Fa' U2 Fa R U' L U2 R' U L' U2
|
|
| 逆算法:L2 D' B U' B U B' D L2 F U' F' |
|
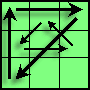 |
左右镜像之逆算法==逆算法之左右镜像:
Fa U2 Fa' L' U R' U2 L U' R U2 |
|
|
左右镜像之逆算法==逆算法之左右镜像: R2 D B' U B' U' B D' R2 F' U F |
|
| N |
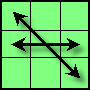 |
(14,17,14,5)
L D' B L' D² R F' R' D² L² B' L' D L'U2 |
|
1/36 |
| (13,18,13,5)
R D' F² L² D' L B² L' D L² F² D R' U |
|
| (14,16,13,5)
L' U R' U² L U' Rs U R'U² L U' R U
|
|
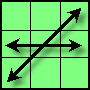 |
左右镜像: R' D B' R D2 L' F L D2 R2 B R D' R U2
|
|
| 左右镜像: L' D F2 R2 D R' B2 R D' R2 F2 D' L U'
|
|
| 左右镜像: R U' L U2 R' U Rs U' L U2 R' U L' U' |
|
如果您有问题,可以在魔方小站论坛发个帖子。
或者,您也可以直接写信给我,任何的只言片语的建议感想都可以的:)我会尽量回复大家。
隐藏/显示工具箱和右下角广告框
|